11 класс
Материалы к зачету по теме "Применение непрерывности и производной"
Понятие о непрерывности функции.
Определение:
Функция f(x) называется непрерывной в точке а, если при стремлении х к а значение f(x) стремится к значению f(a).
Это означает, что для любого числа 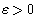 существует такое число существует такое число 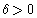 , что для всех х, удовлетворяющих неравенству , что для всех х, удовлетворяющих неравенству 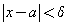 выполняется неравенство выполняется неравенство 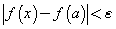 . .
Пример.
Докажем, что линейная функция 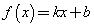 непрерывна в любой точке а. непрерывна в любой точке а.
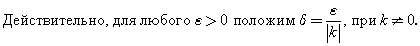
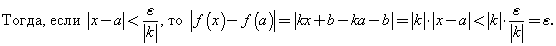
Графическая иллюстрация.
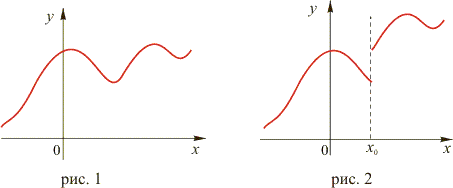
График непрерывной функции представляет собой непрерывную кривую. На рисунках видно, в чём состоит различие между графиком непрерывной функции и графиком так называемой, разрывной функции, которая не является непрерывной.
Применение производной.
Найти уравнение касательной к графику функции 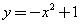 в точке с абсциссой x0 = 1. в точке с абсциссой x0 = 1.
Решение.
1.Найдем производную данной функции: 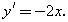
2.Определим значение производной и функции в точке x0 = 1:
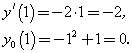
3. По формуле 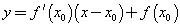 находим уравнение касательной: находим уравнение касательной:
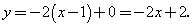
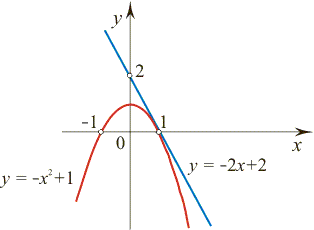
|