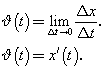алгебра

11 класс

Материалы к зачету по теме "Производная"

Пусть на некотором промежутке задана функция y = f (x); x₀ — приращение аргумента х; точка принадлежит этому промежутку; Δy — приращение функции.

Предел отношения (если он существует) приращения функции Δy к приращению аргумента Δx при стремлении приращения аргумента к нулю называется производной функции в точке x₀, т.е.

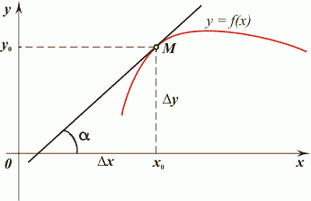
Геометрический смысл производной состоит в том, что значение производной функции в точке x₀ равно угловому коэффициенту касательной (тангенсу угла α ), проведенной к графику функции в точке с абсциссой x₀

где k – угловой коэффициент касательной, или

Пусть материальная точка движется по координатной прямой по закону x = x(t) , т.е. координата этой точки х – известная функция времени t.

Физический смысл производной состоит в том, что производная от координаты по времени есть мгновенная скорость:

Первая формула читается так: "Вэ от тэ равно пределу отношения изменения аргумента к изменению времени, при дэльта тэ стремящимся к нулю. (Здесь предел – от слова limit – лимит).