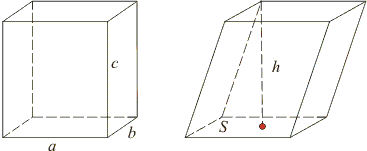12 класс

Материалы к зачетной работе по теме "Объемы многогранников"

Формулы объема многогранников: прямоугольного параллелепипеда, наклонного параллелепипеда, призмы и пирамиды. Примеры.

Теорема: объем прямоугольного параллелепипеда с измерениями а, b, с вычисляется по формуле . Теорема: объем наклонного (любого) параллелепипеда равен произведению площади основания S на высоту h: .

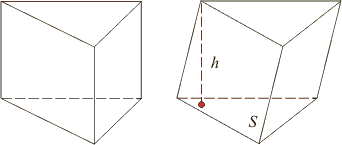Теорема: объем любой призмы равен произведению площади ее основания S на высоту h: .

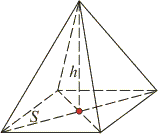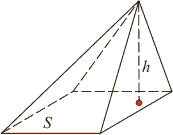Теорема: объем любой пирамиды равен одной трети произведения плошали ее основания S на высоту h: .

Примеры:

1. Куб является прямоугольным параллелепипедом, все измерения которого равны между собой, поэтому объем куба с ребром а равен: .
2. Если в правильной прямой четырехугольной призме провести сечение, которое проходит через диагональ квадрата, лежащего в его основании, и через высоту призмы, то получается две треугольные призмы, объемы которых равны.

вернуться на страницу "Математика"

вверх