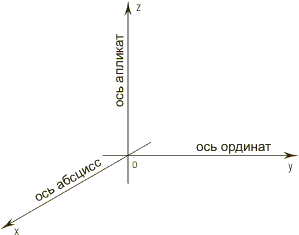11 класс

Материалы к зачетной работе по теме
"Прямоугольная система координат в пространстве. Многогранники"

Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка О – началом координат. Оси координат обозначаются так: Ох, Оу, Oz – и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Oxyz. Три плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Oz, Oz и Ох, называются координатными плоскостями и обозначаются Оху, Oyz, Ozx.

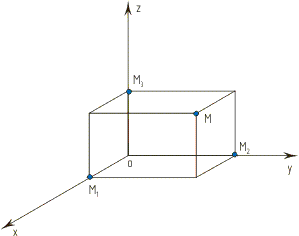В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости. Проведем через точку М три плоскости, перпендикулярные к осям координат, и обозначим через M1, М2 и М3 точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат. Первая координата точки М (она называется абсциссой и обозначается обычно буквой х) определяется так: x = OM1. Аналогично с помощью точки М2 определяется вторая координата (ордината) у точки М, а с помощью точки М3 — третья координата (аппликата) z точки М. Координаты точки М записываются в скобках после обозначения точки: М (х; у; z). Все три координаты начала координат равны нулю: О (0; 0; 0).

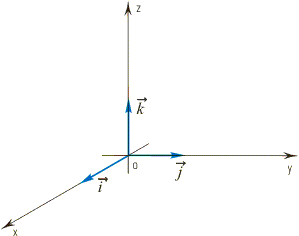Координаты вектора. Зададим в пространстве прямоугольную систему координат Охуz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим через единичный вектор оси абсцисс, через – единичный вектор оси ординат и через – единичный вектор оси аппликат.

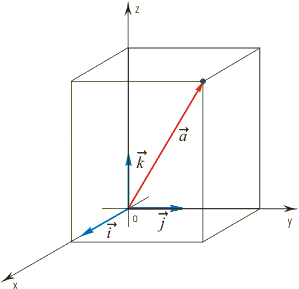Векторы называются координатными векторами. Эти векторы не компланарны, т.е. не лежат в одной плоскости. Поэтому любой вектор можно разложить по координатным векторам, т. е. представить в виде где коэффициенты разложения вектора по координатным осям x, y, z, являются координатами вектора в данной системе координат.

Многогранники

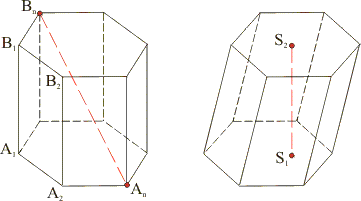Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы (А1А2...Аn и В1В2...Вn), а отрезки, соединяющие соответствующие вершины (А1В1) – боковыми ребрами призмы. Так как параллельный перенос есть движение, то основания призмы равны.

При параллельном переносе плоскость переходит в параллельную плоскость (или в себя), поэтому у призмы основания лежат в параллельных плоскостях.
Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны.
Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми ребрами.
Высотой призмы (S₁S₂) называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы, например А_nВ_n.
Призма называется n-угольной, если ее основания – n-угольники.

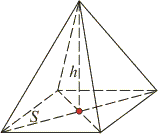Правильной пирамидой называется многогранник, в основании которого лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Все ребра правильной пирамиды равны. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Все апофемы правильной пирамиды равны.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

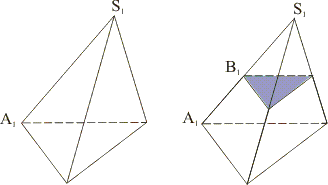В усеченной пирамиде площадь боковой поверхности – это сумма площадей граней пирамиды, которые являются трапециями.

вернуться на страницу "Математика"

вверх