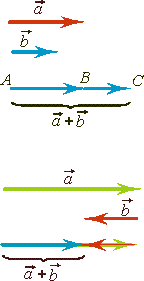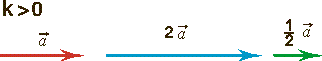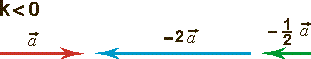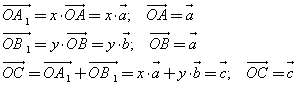Геометрия

10 класс

Материалы к зачетной работе по теме
"Перпендикулярность прямых и плоскостей. Векторы в пространстве"

Параллельный перенос

Введём на плоскости декартовы координаты xОу. Преобразование некоторой фигуры F, при котором произвольная ее точка А (х;у) переходит в другую точку А (х+a; y+b), где а и b постоянные, называется параллельным переносом;
Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

Понятие вектора

Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.

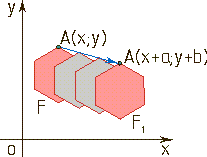Геометрически векторы изображаются направленными отрезками.
Направленный отрезок называется вектором.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).

Если начало вектора — точка А, а его конец — точка В, то вектор обозначается или .

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.

Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Обозначается: .

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора .
Обозначается .

векторы

Два вектора называются равными, если они совмещаются параллельным переносом.
АВСD — параллелограмм,

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы и коллинеарны и их лучи сонаправлены, то векторы и называются сонаправленными.
Обозначаются .
Если векторы и коллинеарны, а их лучи не являются сонаправленными, то векторы и называются противоположно правленными.
Обозначаются . Нулевой вектор условились считать сонаправленным с любым вектором.

коллинеарные векторы:

Свойство коллинеарных векторов

Если векторы и коллинеарны и , то существует число k такое, что . причем если k > 0, то векторы и сонаправленные, если k < 0, то противоположно направленные.

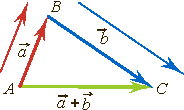
Правило треугольника
Каковы бы ни были точки А, В, С, имеет место векторное равенство:

Рисунки иллюстрируют сложение коллинеарных векторов с помощью параллельного переноса.

Если при сложении векторов и по правилу треугольника точку А заменить другой точкой А₁, то вектор заменится равным ему вектором .

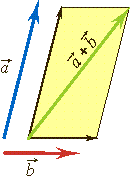
Правило параллелограмма

Если векторы и неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм.
Диагональ параллелограмма есть сумма двух векторов и .

Свойства сложения векторов

Для любых векторов заданных в пространстве, справедливы равенства

	Переместительный закон
	Сочетательный закон

Правило многоугольника применяется, если нужно найти сумму трех или большего числа векторов.
Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
От произвольной точки О отложен вектор затем от точки А отложен вектор и, наконец, от точки В отложен вектор В результате получается вектор

Умножение вектора на число

Произведением ненулевого вектора на число k называется такой вектор, , длина которого равна, , причем векторы и сонаправлены при и противоположно направлены при k < 0.
Произведением нулевого вектора на любое число считается нулевой вектор.

Свойства умножения вектора на число

Для любых векторов и и любых чисел k, m справедливы равенства:

	Сочетательный закон
	Первый распределительный закон
	Второй распределительный закон

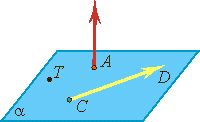
Компланарные векторы

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).

Признак компланарности трех векторов

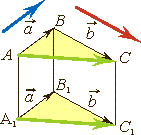
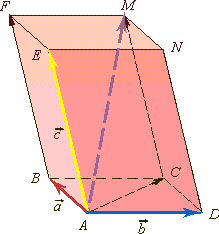
Если вектор можно разложить по векторам и , т.е. представить в виде

где х и у — некоторые числа, то векторы , и компланарны.

Правило параллелепипеда

Сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда, построенному на этих векторах.

Угол между двумя векторами

Углом между двумя направлениями в пространстве называется величина наименьшего угла между любыми лучами этих направлений с общим началом.
Угол между лучами обозначается . По определению угол между двумя направлениями находится в промежутке [0°; 180°].

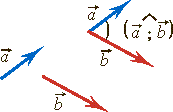Углом между двумя ненулевыми векторами называется угол между направлениями этих векторов.

Перпендикулярные векторы (или ортогональные)	Коллинеарные векторы
Перпендикулярные векторы (или ортогональные)	Сонаправленные	Противоположно направленные

90°	0°	180°

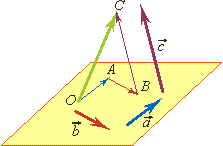
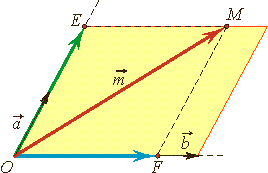
Базис вектора. Разложение вектора на плоскости по двум некомпланарным векторам

Теорема: Любой вектор на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов и :

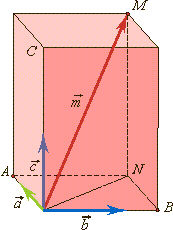
Числа x и y называются координатами вектора. Векторы и называются базисом вектора на плоскости.

Разложение вектора по трем некомпланарным векторам

Базисом пространства называют любые три некомпланарных вектора, взятые в определенном порядке

Теорема: Любой вектор на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов , и :