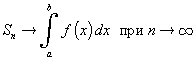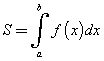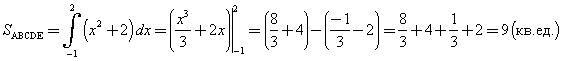12 класс
Материалы к зачету по теме "Интеграл и его применение"
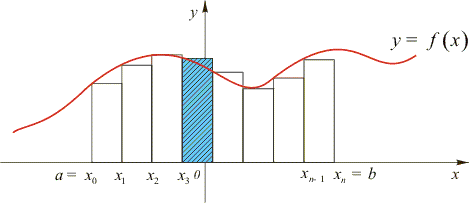
Определение . Разобьем отрезок [a, b] на n отрезков одинаковой длины точками
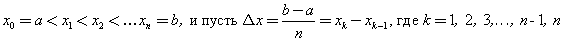 . .
Для любой определенной на отрезке [a, b] функции f (x) рассмотрим сумму, называемую интегральной,
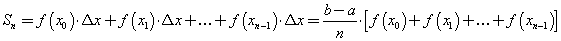 . .
(Для неотрицательной на отрезке [a, b] функции f (x) это сумма площадей всех построенных на отрезках 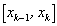 как на основаниях прямоугольников соответственно высотой как на основаниях прямоугольников соответственно высотой 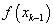 ). ).
Для любой непрерывной на отрезке [a, b] функции f (x) сумма 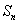 при при 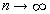 стремится к некоторому числу, которое называют (по определению) интегралом функции f от a до b и обозначают стремится к некоторому числу, которое называют (по определению) интегралом функции f от a до b и обозначают
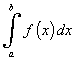 , то есть , то есть 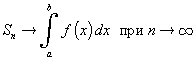
Числа а и b называют пределами интегрирования: а — нижним пределом интегрирования, b — верхним . Знак 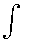 называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования.
Если функция 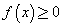 на отрезке [a, b], то площадь S криволинейной трапеции выражается формулой на отрезке [a, b], то площадь S криволинейной трапеции выражается формулой
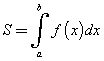
Криволинейной трапецией называется фигура, находящаяся на координатной плоскости и состоящая из всех точек (x,y), удовлетворяющих неравенствам 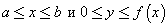 . .
Пример:
Вычислить площадь фигуры, ограниченной линиями: 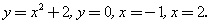
Решение:
1) 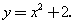 . Графиком этой функции является парабола, вершина которой находится в точке (0; 2), ветви направлены вверх. . Графиком этой функции является парабола, вершина которой находится в точке (0; 2), ветви направлены вверх.
2) х = –1. Графиком этого уравнения является прямая, проходящая через точку (-1; 0) параллельно оси Оу.
3) х = 2. Графиком этого уравнения является прямая, проходящая через точку (2; 0) параллельно оси Оу.
4) у = 0. Графиком этой функции является прямая, совпадающая с осью Ох.
5) Построим графики в одной системе координат:
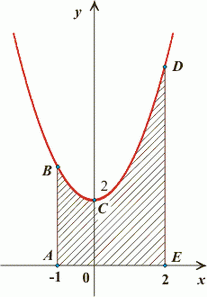
6) Площадь криволинейной трапеции ABCDE определим по формуле Ньютона-Лейбница:
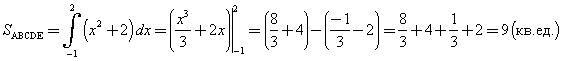
Задание:
Вычислить площадь фигуры, ограниченной линиями: 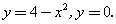
|

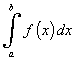 , то есть
, то есть