Определения:
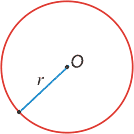
Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки.
Эта точка (О) называется центром окружности.
Расстояние (r) от точки окружности до ее центра называется радиусом окружности.
Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром.
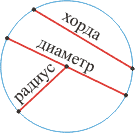
Хорда — отрезок, соединяющий две точки окружности.
Хорда, проходящая через центр окружности, называется диаметром (d=2r).
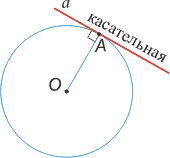
Касательная — прямая (а), проходящая через точку (А) окружности перпендикулярно к радиусу, проведенному в эту точку, называется.
При этом данная точка (А) окружности называется точкой касания.
Часть плоскости, ограниченная окружностью, называется кругом.


Пропорциональные линии в круге
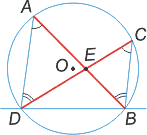
Если две хорды АВ и CD пересекаются внутри круга в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды, т. е.
AЕ·ЕВ = DE·EC
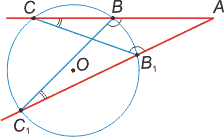
Если из точки, взятой вне окружности, проведены две секущие АС и AC1, то справедливо равенство
AB·AC=АВ1·АС1.
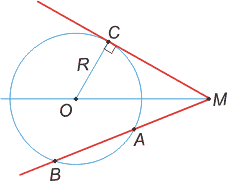
Теорема о квадрате касательной
Если из точки, лежащей вне круга, проведены секущая MB и касательная МС, то справедливо равенство
МC 2 = МВ·МА

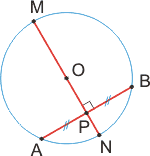
Диаметр окружности, перпендикулярный хорде, проходит через ее середину.
Обратно: если диаметр проходит через середину хорды, то он ей перпендикулярен.

Углы в круге
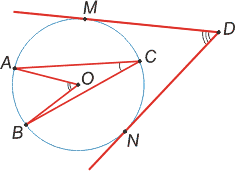
Центральный угол — угол, образованный двумя радиусами (∠AOB).
Вписанный угол — угол, образованный двумя хордами СА и СВ, исходящими из одной точки на окружности (∠ACB).
Описанный угол — угол, образованный двумя касательными DM и DN (∠MDN).
Центральный угол имеет ту же градусную меру, что и дуга, на которую он опирается.
Вписанный угол измеряется половиной дуги, на которую он опирается.
![]()

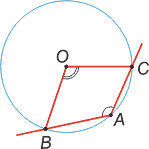
Угол, образованный двумя хордами и опирающийся на них центральный угол связаны соотношением
![]()

Длина окружности
![]()
Длина дуги, соответствующая центральному углу в n°
![]()
Площадь круга
![]()

Круговой сектор — часть круга, лежащая внутри соответствующего центрального угла.
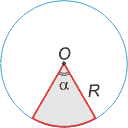
Площадь кругового сектора
![]()
где α — градусная мера угла, R — радиус круга.
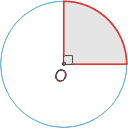
Квадрант — сектор, отсекаемый радиусами, образующими угол 90°.

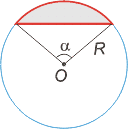
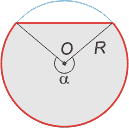
Круговой сегмент — общая часть круга и полуплоскости, граница которой содержит хорду этого круга.
Площадь сегмента, не равного полукругу
![]()
где α — градусная мера центрального угла, которая содержит дугу этого кругового сегмента,
SΔ — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор.
Знак «−» надо брать, когда α<180°, а знак «+», α>180°.
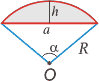
Основание и высота сегмента
![]()

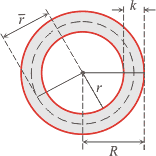
Круговое кольцо
![]()
R, r — внешний и внутренний радиусы;
D, d — внешний и внутренний диаметры;
![]() — средний радиус;
— средний радиус;
k — ширина кольца.