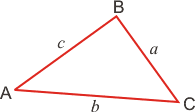
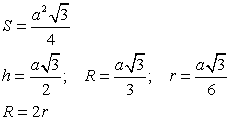Обозначения:
А, В, С — вершины, а также углы при
этих вершинах;
а, b, с — стороны, противолежащие углам
А, В, С соответственно;
ha , hb , hc — высоты, опущенные на стороны
а, b, с соответственно;
ma , mb , mc — медианы;
la , lb , lc — биссектрисы;
R — радиус описанной окружности;
r — радиус вписанной окружности.
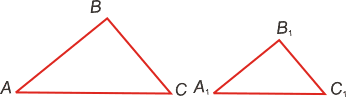
Подобие треугольников
| Признак 1 | Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника.
|
| Признак 2 | Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого и углы, образованные этими сторонами в этих треугольниках, равны.
|
| Признак 3 | Два треугольника подобны, если три стороны одного треугольника пропорциональны сторонам другого треугольника.
|
Прямоугольные треугольники подобны, |
![]()
Если треугольники подобны, то
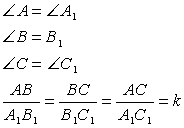
Пропорциональные отрезки в треугольнике
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:
![]()
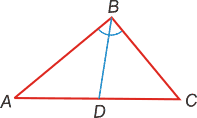

Высотой треугольника
называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.
Высоты треугольника пересекаются в одной точке О, называемой ортоцентром.
В тупоугольном треугольнике ортоцентр лежит вне треугольника.
В прямоугольном он совпадает с вершиной прямого угла.
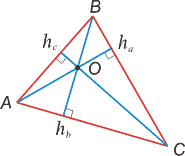
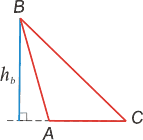

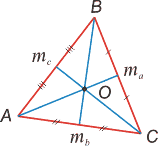
Медианой треугольника
называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника.
Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).

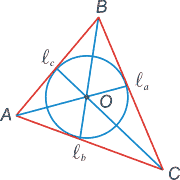
Биссектрисой треугольника
называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной.
Биссектрисой угла называется луч, делящий угол пополам.
Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности.

Равенство треугольников
| Признак 1 | Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
|
| Признак 2 | Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
|
| Признак 3 | Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. |
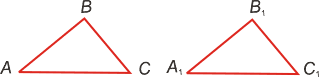
Два треугольника называются равными, если при наложении друг на друга они совместятся.
Если |
то соответственные стороны | |
равны |
||
и соответственные углы равны
![]()

Неавенства треугольника
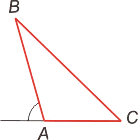
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

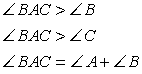

Площадь треугольника
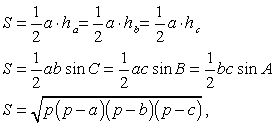
где р — полупериметр треугольника (формула Герона).
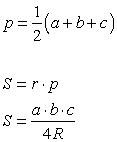

Медиана, биссектриса, высота
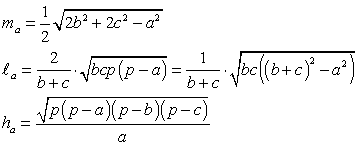

Высоты и стороны треугольника
![]()

Теорема косинусов
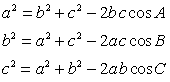

Теорема синусов
![]()

Теорема тангенсов
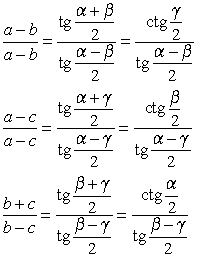

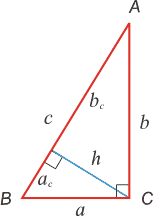
Прямоугольный треугольник
![]()
Теорема Пифагора
![]()
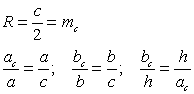

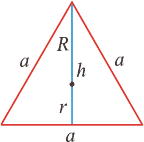
Равносторонний треугольник